Pembagian Pecahan Biasa dan Campuran Dan Contohnya – pembagian pecahan merupakan salah satu ilmu matematika dasar yang biasa dipelajari di kelas 5 dan 6. Dan kali ini akan diulas secara lengkap tentang cara menghitung pembagian pecahan biasa dan pecahan campuran.
Operasi pembagian pecahan memiliki perbedaan dengan pembagian bulangan bulat.
Karena dalam bilangan pecahan ada nilai yang tidak bisa dibulatkan.
Namun konsep dalam pembagian bilangan pecahan dapat di pahami dengan mudah jika teman teman membaca materi kali ini dengan sabar dan teliti.
Oh iya, bagi teman teman yang ingin memiliki materi pembelajaran lainnya. Silahkan kunjungi beberapa tautan berikut ini ya.
Baiklah, langsung saja kita menuju materi utama pada pembahasan kali ini.
Rumus Dasar Pembagian Pecahan
Sebelumnya teman teman perlu tahu istilah “pembilang dan penyebut” pada konsep dasar pembagian pecahan.
Berikut ini penjelasannya.
\(\frac{a}{b}\)
Keterangan !!
- a = Pembilang
- b = penyebut
Jika sudah tahu letak pembilang dan penyebut, maka lanjut ke rumus dalam pembagian bilangan pecahan.
Rumusnya adalah :
Rumus pembagian bilangan pecahan adalah “mengalikan dengan kebalikan pembaginya”.
Contohnya adalah :
\(\frac{a}{b} : \frac{c}{d} = \frac{a}{b}\) x \(\frac{d}{c}\)
Nah, setelah mengetahui dasar konsep pembagian pecahan atau rumusnya.
Selanjutnya kita menuju contoh contoh soal pembagian bilangan pecahan dan bilangan campuran.
Berikut ini ulasannya.
A. Pembagian Pecahan Biasa
Pecahan biasa adalah sebuah bilangan pecahan yang tidak ada nilai genap.
Dalam bilangan pecahan terdapat jenis 2 jenis pecahan, yakni pecahan bilangan biasa dan pecahan bilangan tidak biasa.
Penjelasannya adalah sebagai berikut :
- Pencahan Tidak Biasa : ketika penyebut lebih besar dibangingkan pembilangnya.
- Pencahan Tidak Biasa : ketika pembilang lebih besar dibangingkan penyebutnya.
Dan berikut ini contoh soal dari pembagian pecahan bilangan biasa.
Contoh Soal :
\(\frac{3}{4} : \frac{1}{2} =\) ?
Penyelesaiannya !!
\(\frac{3}{4} : \frac{1}{2} = \frac{3}{4}\) x \(\frac{2}{1} = \frac{6}{4}\)
Karena pecahan \(\frac{6}{4}\) merupakan bilangan pecahan tidak biasa, maka bisa disederhanakan alias bisa diubah ke pecahan campuran.
Berikut ini rumus atau cara mengubah pecah tidak biasa ke pecahan campuran.
\(\frac{3}{4} : \frac{1}{2} = \frac{3}{4}\) x \(\frac{2}{1} = \frac{6}{4} = \frac{3}{2}\) = 1\(\frac{1}{2}\)
– Jadi pecahan \(\frac{6}{4}\) jika disederhanakan akan menjadi 1\(\frac{1}{2}\)
Nilai tersebut didapat dari perhitungan berikut :

B. Rumus Pembagian Bilangan Bulat dengan Bilangan Pecahan
Lalu bagimana cara membagi bilangan bulat ke bilangan pecahan atau sebaliknya ?
Berikut ini penjelasan dan contoh soalnya.
Perlu di garis bawahi terlebih dahulu.
Rumus Pembagian Bilangan Bulat dengan Bilangan Pecahan atau sebaliknya adalah :
1. Cara menghitungnya sama seperti bilangan pecahan.
2. Namun bilangan bulat diubah dahulu ke dalam bentuk bilangan pecahan dengan menambahkan nilai penyebut = “\(\frac{x}{1}\)“.
Dengan rumus tersebut maka kita bisa menyelesaikan soal berikut ini.
\(\frac{3}{8}\) : 2 = ?
Penyelesaiannya !!
– Rubah dulu bilangan bulat (2) ke pecahan campuran.
– Setelah itu, gunakan rumus pembagian bilangan pecahan.
\(\frac{3}{8} : \frac{2}{1} = \frac{3}{8}\) x \(\frac{1}{2} = \frac{3}{16}\)
Karena \(\frac{3}{16}\) merupakan pecahan biasa, yang mana pembilangnya memiliki nilai lebih kecil dari pada penyebutnya, maka hasilnya tetap \(\frac{3}{16}\).
Ok, itu tadi penjelasan cara pembagian bilangan bulat dengan bilangan pecahan.
Selanjutnya kita bahas bagaimana cara membagi bilangan pecahan campuran dengan bilangan pecahan campuran.
C. Rumus Pembagian Bilangan Pecahan Campuran dengan Bilangan Pecahan Campuran
Pada dasarnya, bilangan pecahan campuran itu adalah bentuk dari bilangan pecahan tidak biasa.
Untuk itu, rumusnya adalah sebagai berikut :
1. Untuk rumus pembagian jenis bilangan campuran, maka teman teman bisa mengubah bilangan campuran tersebut kedalam bilangan pecahan tidak biasa(semuanya).
2. Cara mengubah pecahan campuran ke pecahan tidak biasa adalah dengan mengalikan peyebutnya.
Nah, untuk memahaminya silahkan lihat contoh soalnya berikut ini.
Contoh Soal :
3\(\frac{4}{5}\) : 1\(\frac{1}{2}\) = ?
Cara mengerjakannya !!
– Rubah dahulu pecahan campuran tersebut kedalam bilangan pecahan tidak biasa.
– Setelah itu, gunakan rumus pembagian bilangan pecahan.
3\(\frac{4}{5}\) : 1\(\frac{1}{2}\) =
3\(\frac{4}{5}\) = \(\frac{\left ( 3×5 \right )+4}{5}=\frac{15+4}{5}=\frac{19}{5}\)
1\(\frac{1}{2}\) = \(\frac{\left ( 1×2 \right )+1}{2}=\frac{2+1}{2}=\frac{3}{2}\)
Dari perubahan diatas, maka diperoleh nilai sebagai berikut :
3\(\frac{4}{5}\) : 1\(\frac{1}{2}\) =\(\frac{19}{5}\) : \(\frac{3}{2}\)
= \(\frac{19}{5}\) x \(\frac{2}{3}\)
= \(\frac{38}{15}\)
Karena \(\frac{38}{15}\) adalah pecahan tidak biasa, maka bisa diubah ke dalam bentuk sederhana.
Rumus mengubahnya adalah sebagai berikut :
3\(\frac{4}{5}\) : 1\(\frac{1}{2}\) = \(\frac{19}{5}\) : \(\frac{3}{2}\) = \(\frac{19}{5}\) x \(\frac{2}{3}\) = \(\frac{38}{15}\) = 2 \(\frac{8}{15}\)
Nilai diatas didapat dari :
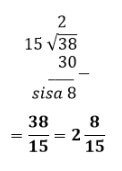
Untuk teman teman yang ingin mendapatkan rangkuman inti dari tema kali ini, silahkan dowload filenya berikut ini.
Download Rumus Pembagian Bilangan Pecahan dan Campuran
Silahkan lihat tabel daftarnya berikut ini.
| Judul | Link |
|---|---|
| Rumus dasar pembagian bilangan pecahan.doc | Download |
| Rumus dasar pembagian bilangan pecahan.pdf | Download |
Ok, itu tadi penjelasan lengkap dari tema Pembagian Pecahan Biasa dan Campuran serta Contoh soal yang bisa teman teman pelajari untuk memahami setiap rumus.
Sampai disini dulu, jika ada pertanyaan seputar materi kali ini silahkan tulis dikolom komentar ya.
